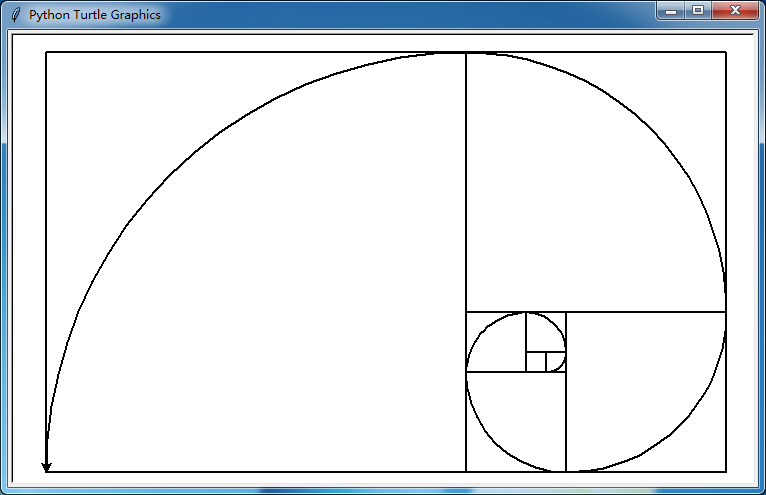
螺旋线
人家要我去学阿基米德螺旋线,但显然我是数学渣,根本领会到不到那些精神,转换不过来,就不要装着能转换。既然习题5说“或者其他种类的螺线”于是我就选择了在我理解范围内的斐波那契螺旋线,也就是黄金螺旋线。人家要我画螺旋线,我觉得要把方框也画出来才容易验证我自己有没有搞错。
为了完成方形和圆弧的两个循环,我笨蛋地把斐波那契数列算了两次……
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 | import turtle, math def arc(t, r, angle): n = 20 # int(2*math.pi*r/4)+3 公式画图太细致太慢,直接赋值加速 step_length = int(2*math.pi*r)*angle/360/n step_angle = angle/n t.lt(step_angle/2) # 据说折腾一下角度能消除像素误差? polygon(t, step_length, n, step_angle) t.rt(step_angle/2) def polygon(t, length, n, angle): for i in range(n): t.fd(length) t.lt(angle) def start(t): # 起点要先偏移一些,每次方向保持一致 t.pu() t.home() t.goto(160,-110) def square(t, size): # 第一个正方形 for i in range(4): t.lt(90) t.fd(size) t.rt(90) def boxes(t, n, size): # n-1个正方形 a = b = 1 base = size for i in range(n-1): for i in range(6): t.lt(90) t.fd(size) t.rt(90) fibo = a+b # 计算斐波那契数列 a = b b = fibo size = base*fibo def spiral(t, n, size): # 第一个正方形里没有弧线,所以弧线也是n-1 a = b = 1 base = size for i in range(n-1): arc(t, size, 90) fibo = a+b # 在算一次斐波那契数列 a = b b = fibo size = base*fibo bob = turtle.Turtle() bob.pensize(2) # 笔迹粗点好看些 n = 8 size = 20 start(bob) square(bob, size) boxes(bob, n, size) start(bob) spiral(bob, n, size) turtle.mainloop() |