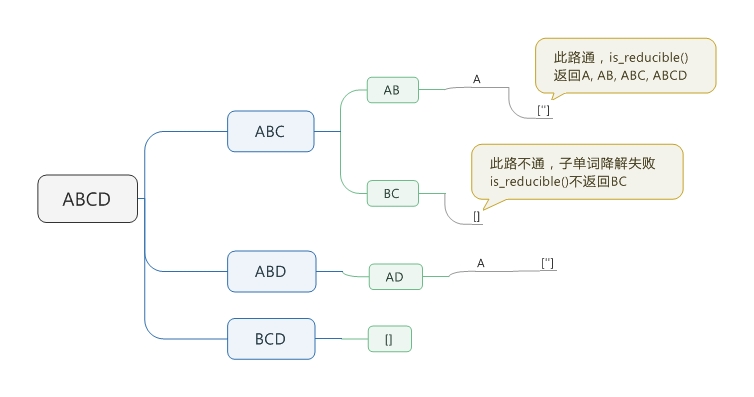
觉得自己虽然见过递归,但几乎不用,不逼着我我都不用,循环用得越来越遛。前两题我和参考答案得出的结论一致,最后一题,我觉得参考答案有问题。下面的都是我的脚本。下面要用到的words.txt在这里。
Exercise 7:This question is based on a Puzzler that was broadcast on the radio program Car Talk: Give me a word with three consecutive double letters. I’ll give you a couple of words that almost qualify, but don’t. For example, the word committee, c-o-m-m-i-t-t-e-e. It would be great except for the ‘i’ that sneaks in there. Or Mississippi: M-i-s-s-i-s-s-i-p-p-i. If you could take out those i’s it would work. But there is a word that has three consecutive pairs of letters and to the best of my knowledge this may be the only word. Of course there are probably 500 more but I can only think of one. What is the word? Write a program to find it. Solution: http://thinkpython2.com/code/cartalk1.py.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| def double_letter(word):
num = 0
i = 0
if len(word) >= 6:
while i < len(word)-1:
if word[i] == word[i+1]:
num = num + 1
i = i + 2
elif i > 2 and word[i-2] != word[i-3]:
break
else:
i = i + 1
if num == 3:
print(word)
fin = open('words.txt')
n = 0
for line in fin:
word = line.strip()
double_letter(word)
# bookkeeper
# bookkeepers
# bookkeeping
# bookkeepings |
def double_letter(word):
num = 0
i = 0
if len(word) >= 6:
while i < len(word)-1:
if word[i] == word[i+1]:
num = num + 1
i = i + 2
elif i > 2 and word[i-2] != word[i-3]:
break
else:
i = i + 1
if num == 3:
print(word)
fin = open('words.txt')
n = 0
for line in fin:
word = line.strip()
double_letter(word)
# bookkeeper
# bookkeepers
# bookkeeping
# bookkeepings
Exercise 8: Here’s another Car Talk Puzzler: “I was driving on the highway the other day and I happened to notice my odometer. Like most odometers, it shows six digits, in whole miles only. So, if my car had 300,000 miles, for example, I’d see 3-0-0-0-0-0. “Now, what I saw that day was very interesting. I noticed that the last 4 digits were palindromic; that is, they read the same forward as backward. For example, 5-4-4-5 is a palindrome, so my odometer could have read 3-1-5-4-4-5. “One mile later, the last 5 numbers were palindromic. For example, it could have read 3-6-5-4-5-6. One mile after that, the middle 4 out of 6 numbers were palindromic. And you ready for this? One mile later, all 6 were palindromic! “The question is, what was on the odometer when I first looked?” Write a Python program that tests all the six-digit numbers and prints any numbers that satisfy these requirements. Solution: http://thinkpython2.com/code/cartalk2.py.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| def is_palindrome(word):
if word[::-1] == word:
return True
def test_palindrome(number):
if is_palindrome(str(number)[2:]):
if is_palindrome(str(number+1)[1:]):
if is_palindrome(str(number+2)[1:1]):
if is_palindrome(str(number+3)):
return True
for number in range(100000, 999999):
if test_palindrome(number):
print(number)
# 198888
# 199999 |
def is_palindrome(word):
if word[::-1] == word:
return True
def test_palindrome(number):
if is_palindrome(str(number)[2:]):
if is_palindrome(str(number+1)[1:]):
if is_palindrome(str(number+2)[1:1]):
if is_palindrome(str(number+3)):
return True
for number in range(100000, 999999):
if test_palindrome(number):
print(number)
# 198888
# 199999
Exercise 9: Here’s another Car Talk Puzzler you can solve with a search: “Recently I had a visit with my mom and we realized that the two digits that make up my age when reversed resulted in her age. For example, if she’s 73, I’m 37. We wondered how often this has happened over the years but we got sidetracked with other topics and we never came up with an answer. “When I got home I figured out that the digits of our ages have been reversible six times so far. I also figured out that if we’re lucky it would happen again in a few years, and if we’re really lucky it would happen one more time after that. In other words, it would have happened 8 times over all. So the question is, how old am I now?” Write a Python program that searches for solutions to this Puzzler. Hint: you might find the string method zfill useful. Solution: http://thinkpython2.com/code/cartalk3.py.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| year = 99
meet = int(input('how many times have we met?(1-8): '))
print('mom born me at', '\t','my age', '\t',"mon's age")
for i in range(10, 80): # 假设你妈生你的最低年龄是10,最高年龄是80
n = 0
for age in range(1, year):
if age < int(str(age).zfill(2)[::-1]) and int(str(age).zfill(2)[::-1]) - age == i:
# print(i, '\t\t', age, '\t\t', str(age).zfill(2)[::-1])
n = n + 1
if n == meet:
print(i, '\t\t', age, '\t\t', str(age).zfill(2)[::-1])
# how many times have we met?(1-8): 6
# mom born me at my age mon's age
# 18 57 75
# 27 58 85
# 36 59 95
# how many times have we met?(1-8): 8
# mom born me at my age mon's age
# 18 79 97
# mom born me at my age mon's age
# 18 2 20
# 18 13 31
# 18 24 42
# 18 35 53
# 18 46 64
# 18 57 75
# 18 68 86
# 18 79 97
# 27 3 30
# 27 14 41
# 27 25 52
# 27 36 63
# 27 47 74
# 27 58 85
# 27 69 96
# 36 4 40
# 36 15 51
# 36 26 62
# 36 37 73
# 36 48 84
# 36 59 95
# 45 5 50
# 45 16 61
# 45 27 72
# 45 38 83
# 45 49 94
# 54 6 60
# 54 17 71
# 54 28 82
# 54 39 93
# 63 7 70
# 63 18 81
# 63 29 92
# 72 8 80
# 72 19 91 |
year = 99
meet = int(input('how many times have we met?(1-8): '))
print('mom born me at', '\t','my age', '\t',"mon's age")
for i in range(10, 80): # 假设你妈生你的最低年龄是10,最高年龄是80
n = 0
for age in range(1, year):
if age < int(str(age).zfill(2)[::-1]) and int(str(age).zfill(2)[::-1]) - age == i:
# print(i, '\t\t', age, '\t\t', str(age).zfill(2)[::-1])
n = n + 1
if n == meet:
print(i, '\t\t', age, '\t\t', str(age).zfill(2)[::-1])
# how many times have we met?(1-8): 6
# mom born me at my age mon's age
# 18 57 75
# 27 58 85
# 36 59 95
# how many times have we met?(1-8): 8
# mom born me at my age mon's age
# 18 79 97
# mom born me at my age mon's age
# 18 2 20
# 18 13 31
# 18 24 42
# 18 35 53
# 18 46 64
# 18 57 75
# 18 68 86
# 18 79 97
# 27 3 30
# 27 14 41
# 27 25 52
# 27 36 63
# 27 47 74
# 27 58 85
# 27 69 96
# 36 4 40
# 36 15 51
# 36 26 62
# 36 37 73
# 36 48 84
# 36 59 95
# 45 5 50
# 45 16 61
# 45 27 72
# 45 38 83
# 45 49 94
# 54 6 60
# 54 17 71
# 54 28 82
# 54 39 93
# 63 7 70
# 63 18 81
# 63 29 92
# 72 8 80
# 72 19 91