2020-04
10

强大到让我瑟瑟发抖的递归

By xrspook @ 8:41:56 归类于: 烂日记

大学学习C语言的时候，基本上我不会写单独的函数，所有要解决的事都在主函数里搞定了。当时我学过判断和循环，但是，我却从来没学过递归。在解决一些简单事情的时候，循环跟递归，没什么差别。从理解程度来说，我觉得循环更简洁一些，但是，当某个东西像套娃那样一层叠一层，每层里面依然用同样的规则继续套叠，不知道要叠多少层的时候。递归就会展现它无穷的魔力。循环难以实现这个，又或者循环并非实现不了，但是递归在完全不需要体现循环的框架下，简洁的语言就已经在做着循环的事情。

昨天，我第一次在Python里见到这个恐怖的递归。外国人的书，我觉得都有一个特点。正文的时候举的例子都很简单，但是一到习题，就会把你彻底搞死。习题里面会偷偷带入一些超纲的东西。大概写书的人理所当然默认你应该知晓。这种事情我已经在学习Java的时候领略过。当时那本书之所以没法看下去，就是因为我没办法想象出作者的脑洞到底是什么。他们的习题几乎可以说大多是一些填空题，但要实现一个功能，其实未必一定就得用某种方法。你给我一个条件，给我一些目标值，我能做出来也就OK了，为啥必须走你的路呢，这非常难。之前我不觉得自己跟外国人的脑洞到底差多远，但是当我对比过自己和他们写的程序以后，我发现真的差挺远的。虽然我们都能实现某个功能，就效率而言，感觉上没差多少，因为我只是在做一些非常初级的东西。应试教育的时候，有标准答案，当然好判定成绩，但实际上，编程这种东西真心应该天马行空。给我一个效率的限制，比如说完成某件事，必须在多长时间之内解决，代码长度不能多于多少，至于我用什么办法，这是我的事。

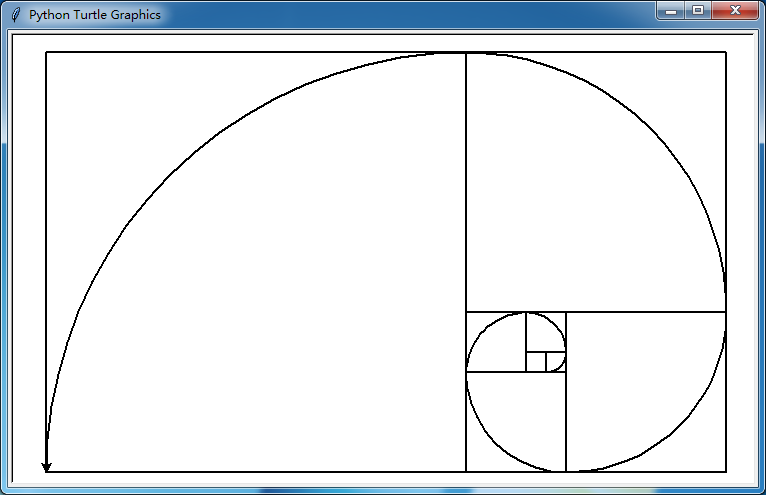
说回递归函数这件事，在处理几个简单数字的时候，可能你感觉不到它的强大，但是，当我见识过用那个东西画出来的层级图形以后，我简直就只有站在旁边瑟瑟发抖的份儿。真的不知道是哪个神经质想出来这么强大的东西。但实际上，深究下去，那也不是很强大，那不过是不断地重复一些已经设计好的事情而已。如果要人去做那些重复，一开始还好，但是随着事情的深入，会慢慢乱套，但是计算机不会，他们会一根筋地执行我们的指令。最终出来的结果是令人惊叹的优雅，还是乱七八糟一坨屎：就得看设定规律的人的功力了。

递归现在对我来说是一个非常恐怖的东西。因为我不了解它，所以我害怕它，就像当年认识循环一样。但是，用好递归以后，我的武器库里就会增加一个杀伤性非常大的家伙。说到递归，让我联想起新冠病毒。这个东西的递归到底什么时候才是个头？我觉得这肯定不是一个死循环，自然界非常擅长递归，处处都是数学和逻辑你知道吗？！但是，到底要递归多少次，全人类才最终能看到隧道尽头的曙光呢？到底这个新冠病毒函数的递归里埋伏了多少个随机数呢？学习递归让我明白到，层级少好对付，层级一旦扩增，那就是次数级的增长，而且，说不准到达一定层级的以后就会触发某些大招炸弹，想想都心寒。

编程是一个让我重新理解自然规律的过程。

标签：, , , , , , , , , , , , ,
4 条评论
2020-04
9

转换时间戳

By xrspook @ 15:18:47 归类于: 扮IT

脑袋实在转不过来，不知道怎么把1W多天转化为月份，长短月怎么处理？？？？？所以直接暴力地使用本来就内置的time.localtime()以及time.strftime()格式化当前时间。我完全可以把逝去的时间也这么整，但逝去时间我是有认真人肉计算过的，所以同一个时间戳，用了两种方式转化。

经过这个以后，我完全明白点点导出数据里那一串标记着的数字是什么鬼，也不能说他们这样不好，因为转化为实在人肉可读的时间格式以后万一要用其它表达方式呢？一开始就用最原始的东西，前端表达用内置的函数格式化也就可以了。所以，大概看懂的人会会心微笑，看不懂的人会骂街。作为理论上应该可读的XML文件，他们这般“原始输出”实在够姜！

1
2
3
4
5
6
7
8
9
10
11
12
13

import time
def now(num):
    mytime = time.strftime("%Y-%m-%d %H:%M:%S", time.localtime(num))
    return(str(mytime))
num = int(time.time())
sec = num % 60
min = (num // 60) % 60
hour = (num // (60 * 60)) % 24 + 8 # 万恶的东八区！！！！！！！！！！
day = num // (60 * 60 * 24)
print('Time is', now(num))
print('since the epoch, ' + str(day) + ' days ' + str(hour) + ' hours ' + str(min) + ' minutes ' + str(sec) + ' seconds has gone')
# Time is 2020-04-09 15:03:41
# since the epoch, 18361 days 15 hours 3 minutes 41 seconds has gone

标签：, , , , , , ,
2 条评论
2020-04
8

螺旋线

By xrspook @ 20:29:37 归类于: 扮IT

人家要我去学阿基米德螺旋线，但显然我是数学渣，根本领会到不到那些精神，转换不过来，就不要装着能转换。既然习题5说“或者其他种类的螺线”于是我就选择了在我理解范围内的斐波那契螺旋线，也就是黄金螺旋线。人家要我画螺旋线，我觉得要把方框也画出来才容易验证我自己有没有搞错。

为了完成方形和圆弧的两个循环，我笨蛋地把斐波那契数列算了两次……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

import turtle, math
def arc(t, r, angle):
    n = 20 # int(2*math.pi*r/4)+3 公式画图太细致太慢，直接赋值加速
    step_length = int(2*math.pi*r)*angle/360/n
    step_angle = angle/n
    t.lt(step_angle/2) # 据说折腾一下角度能消除像素误差？
    polygon(t, step_length, n, step_angle)
    t.rt(step_angle/2)
def polygon(t, length, n, angle):
    for i in range(n):
        t.fd(length)
        t.lt(angle)
def start(t): # 起点要先偏移一些，每次方向保持一致
    t.pu()
    t.home()
    t.goto(160,-110)
def square(t, size): # 第一个正方形
    for i in range(4):
        t.lt(90)
        t.fd(size)                
    t.rt(90)
def boxes(t, n, size): # n-1个正方形
    a = b = 1
    base = size
    for i in range(n-1):
        for i in range(6):
            t.lt(90)
            t.fd(size)
        t.rt(90)
        fibo = a+b # 计算斐波那契数列
        a = b
        b = fibo
        size = base*fibo
def spiral(t, n, size): # 第一个正方形里没有弧线，所以弧线也是n-1
    a = b = 1
    base = size
    for i in range(n-1):
        arc(t, size, 90)        
        fibo = a+b # 在算一次斐波那契数列
        a = b
        b = fibo
        size = base*fibo
bob = turtle.Turtle()
bob.pensize(2) # 笔迹粗点好看些
n = 8
size = 20
start(bob)
square(bob, size)
boxes(bob, n, size)
start(bob)
spiral(bob, n, size)
turtle.mainloop()
标签：, , , , ,
还没有评论
2020-04
8

冷静不慌了

By xrspook @ 13:49:05 归类于: 扮IT

昨晚的习题2的花朵让我很郁闷，今天习题3的PIE我沉着冷静了，所以快速完成任务。

跟参考答案用的不是一个画法，我先画中间的梗，再画外面的框，参考答案是一个接一个三角形画。无论哪个，都逃不掉三角形边长的正弦计算，你叫小学生怎么画！！！两种画法如果设定的内径一样，画出的线条长度是一样的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import turtle, math
def pie(t, r, n): # t for turtle, r for radius, n for sides
    angle = 360/n
    for i in range(n):
        bob.fd(r)
        bob.bk(r)
        bob.lt(angle)
    bob.fd(r)
    bob.lt(180-(180-angle)/2)
    for i in range(n):    
        bob.fd(2*math.sin(math.radians(angle/2))*r)
        bob.lt(angle)
    bob.rt(180-(180-angle)/2)
def move(t, length): # t for turle
    t.pu()
    t.fd(length)
    t.pd()
bob = turtle.Turtle()
move(bob, -230)
pie(bob, 100, 5)
move(bob, 120)
pie(bob, 100, 6)
move(bob, 120)
pie(bob, 100, 7)
turtle.mainloop()
标签：, , , , , ,
还没有评论
2020-04
7

阴魂不散的小海龟

By xrspook @ 21:56:27 归类于: 扮IT

LOGO语言小海龟,你为啥阴魂不散啊啊啊啊啊啊啊啊啊啊！！！！！对从前小学3年级的我来说是个噩梦，现在依然是个噩梦！Think Python 2的第四章正是用这个turtle讲故事，想死的心都有了。没有一定英语基础，没有足够强悍的数学基础，怎么可能玩得转小海龟，而且还要空间思维能力。小时候我对这个东西瑟瑟发抖实在太正常了…… 25年后再遇到，我继续纠结得死去活来……

第四章最后的习题1要求画一个堆栈图，不知道他们到底要画些什么，要画到什么程度，mindmanager了一个，画完以后的确对函数的嵌套有点开窍。

习题2要画3朵花，画得我死去活来…… 但总算完全不看答案能画出来，看完答案，得到那些偷偷摸摸设定的参数后能画得跟要求一模一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

import turtle, math
def arc(t, r, angle):
    n = 20 # int(2*math.pi*r/4)+3 公式画图太细致太慢，直接赋值加速
    step_length = int(2*math.pi*r)*angle/360/n
    step_angle = angle/n
    t.lt(step_angle/2) # 据说折腾一下角度能消除像素误差？
    polygon(t, step_length, n, step_angle)
    t.rt(step_angle/2)
def polygon(t, length, n, angle):
    for i in range(n):
        t.fd(length)
        t.lt(angle)
def flower(t, p, r, a): # t for turtle, p for petal, r for radius, a for angle
    for i in range(p):
        for i in range(2): # 重复两次画花瓣，两次转向后和初始方向一致，非常重要！！！！！
            arc(t, r, a)
            t.lt(180-a)
        t.lt(360/p)
def move(t, length): # 一个画板画3朵花必须用暗中位移
    t.pu()
    t.fd(length)
    t.pd()
bob = turtle.Turtle()
move(bob, -100)
flower(bob, 7, 60, 60) # 偷偷设定半径和角度，万恶的例子，叫人怎么猜！于是我也直接搬！
move(bob, 100)
flower(bob, 10, 40, 80)
move(bob, 100)
flower(bob, 20, 140, 20)
turtle.mainloop()
标签：, , , , , , , , , , , , ,
还没有评论
1 … 36 37 38 39 40 41 42 43 44 … 132
© 2004 - 2024 我的天 | Theme by xrspook | Power by WordPress
Go to top