2020-04
9

转换时间戳

By xrspook @ 15:18:47 归类于: 扮IT

脑袋实在转不过来，不知道怎么把1W多天转化为月份，长短月怎么处理？？？？？所以直接暴力地使用本来就内置的time.localtime()以及time.strftime()格式化当前时间。我完全可以把逝去的时间也这么整，但逝去时间我是有认真人肉计算过的，所以同一个时间戳，用了两种方式转化。

经过这个以后，我完全明白点点导出数据里那一串标记着的数字是什么鬼，也不能说他们这样不好，因为转化为实在人肉可读的时间格式以后万一要用其它表达方式呢？一开始就用最原始的东西，前端表达用内置的函数格式化也就可以了。所以，大概看懂的人会会心微笑，看不懂的人会骂街。作为理论上应该可读的XML文件，他们这般“原始输出”实在够姜！

1
2
3
4
5
6
7
8
9
10
11
12
13

import time
def now(num):
    mytime = time.strftime("%Y-%m-%d %H:%M:%S", time.localtime(num))
    return(str(mytime))
num = int(time.time())
sec = num % 60
min = (num // 60) % 60
hour = (num // (60 * 60)) % 24 + 8 # 万恶的东八区！！！！！！！！！！
day = num // (60 * 60 * 24)
print('Time is', now(num))
print('since the epoch, ' + str(day) + ' days ' + str(hour) + ' hours ' + str(min) + ' minutes ' + str(sec) + ' seconds has gone')
# Time is 2020-04-09 15:03:41
# since the epoch, 18361 days 15 hours 3 minutes 41 seconds has gone

标签：, , , , , , ,
2 条评论
2020-04
8

螺旋线

By xrspook @ 20:29:37 归类于: 扮IT

人家要我去学阿基米德螺旋线，但显然我是数学渣，根本领会到不到那些精神，转换不过来，就不要装着能转换。既然习题5说“或者其他种类的螺线”于是我就选择了在我理解范围内的斐波那契螺旋线，也就是黄金螺旋线。人家要我画螺旋线，我觉得要把方框也画出来才容易验证我自己有没有搞错。

为了完成方形和圆弧的两个循环，我笨蛋地把斐波那契数列算了两次……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

import turtle, math
def arc(t, r, angle):
    n = 20 # int(2*math.pi*r/4)+3 公式画图太细致太慢，直接赋值加速
    step_length = int(2*math.pi*r)*angle/360/n
    step_angle = angle/n
    t.lt(step_angle/2) # 据说折腾一下角度能消除像素误差？
    polygon(t, step_length, n, step_angle)
    t.rt(step_angle/2)
def polygon(t, length, n, angle):
    for i in range(n):
        t.fd(length)
        t.lt(angle)
def start(t): # 起点要先偏移一些，每次方向保持一致
    t.pu()
    t.home()
    t.goto(160,-110)
def square(t, size): # 第一个正方形
    for i in range(4):
        t.lt(90)
        t.fd(size)                
    t.rt(90)
def boxes(t, n, size): # n-1个正方形
    a = b = 1
    base = size
    for i in range(n-1):
        for i in range(6):
            t.lt(90)
            t.fd(size)
        t.rt(90)
        fibo = a+b # 计算斐波那契数列
        a = b
        b = fibo
        size = base*fibo
def spiral(t, n, size): # 第一个正方形里没有弧线，所以弧线也是n-1
    a = b = 1
    base = size
    for i in range(n-1):
        arc(t, size, 90)        
        fibo = a+b # 在算一次斐波那契数列
        a = b
        b = fibo
        size = base*fibo
bob = turtle.Turtle()
bob.pensize(2) # 笔迹粗点好看些
n = 8
size = 20
start(bob)
square(bob, size)
boxes(bob, n, size)
start(bob)
spiral(bob, n, size)
turtle.mainloop()
标签：, , , , ,
还没有评论
2020-04
8

冷静不慌了

By xrspook @ 13:49:05 归类于: 扮IT

昨晚的习题2的花朵让我很郁闷，今天习题3的PIE我沉着冷静了，所以快速完成任务。

跟参考答案用的不是一个画法，我先画中间的梗，再画外面的框，参考答案是一个接一个三角形画。无论哪个，都逃不掉三角形边长的正弦计算，你叫小学生怎么画！！！两种画法如果设定的内径一样，画出的线条长度是一样的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import turtle, math
def pie(t, r, n): # t for turtle, r for radius, n for sides
    angle = 360/n
    for i in range(n):
        bob.fd(r)
        bob.bk(r)
        bob.lt(angle)
    bob.fd(r)
    bob.lt(180-(180-angle)/2)
    for i in range(n):    
        bob.fd(2*math.sin(math.radians(angle/2))*r)
        bob.lt(angle)
    bob.rt(180-(180-angle)/2)
def move(t, length): # t for turle
    t.pu()
    t.fd(length)
    t.pd()
bob = turtle.Turtle()
move(bob, -230)
pie(bob, 100, 5)
move(bob, 120)
pie(bob, 100, 6)
move(bob, 120)
pie(bob, 100, 7)
turtle.mainloop()
标签：, , , , , ,
还没有评论
2020-04
7

阴魂不散的小海龟

By xrspook @ 21:56:27 归类于: 扮IT

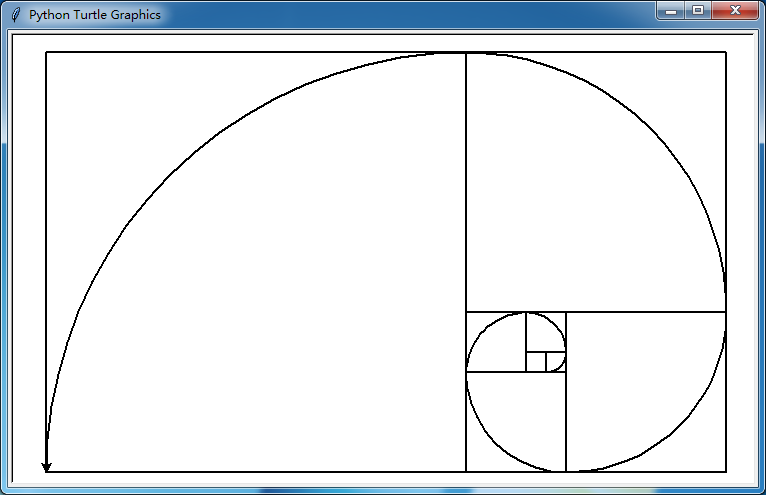
LOGO语言小海龟,你为啥阴魂不散啊啊啊啊啊啊啊啊啊啊！！！！！对从前小学3年级的我来说是个噩梦，现在依然是个噩梦！Think Python 2的第四章正是用这个turtle讲故事，想死的心都有了。没有一定英语基础，没有足够强悍的数学基础，怎么可能玩得转小海龟，而且还要空间思维能力。小时候我对这个东西瑟瑟发抖实在太正常了…… 25年后再遇到，我继续纠结得死去活来……

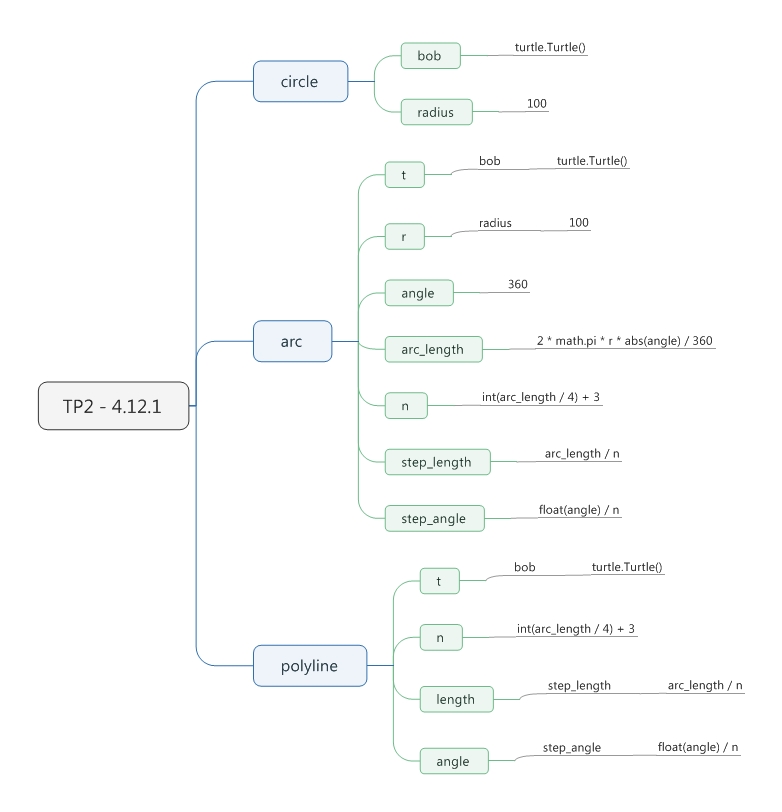
第四章最后的习题1要求画一个堆栈图，不知道他们到底要画些什么，要画到什么程度，mindmanager了一个，画完以后的确对函数的嵌套有点开窍。

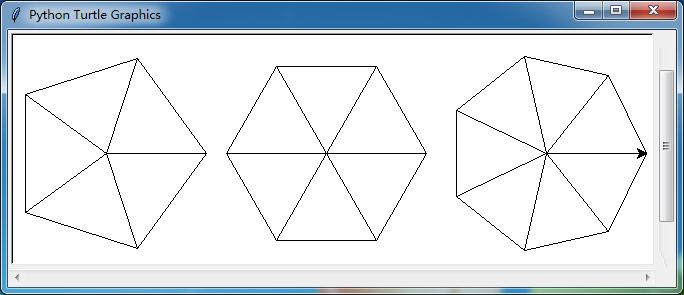
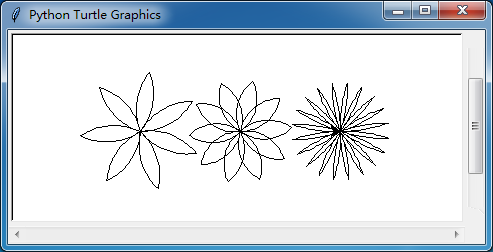
习题2要画3朵花，画得我死去活来…… 但总算完全不看答案能画出来，看完答案，得到那些偷偷摸摸设定的参数后能画得跟要求一模一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

import turtle, math
def arc(t, r, angle):
    n = 20 # int(2*math.pi*r/4)+3 公式画图太细致太慢，直接赋值加速
    step_length = int(2*math.pi*r)*angle/360/n
    step_angle = angle/n
    t.lt(step_angle/2) # 据说折腾一下角度能消除像素误差？
    polygon(t, step_length, n, step_angle)
    t.rt(step_angle/2)
def polygon(t, length, n, angle):
    for i in range(n):
        t.fd(length)
        t.lt(angle)
def flower(t, p, r, a): # t for turtle, p for petal, r for radius, a for angle
    for i in range(p):
        for i in range(2): # 重复两次画花瓣，两次转向后和初始方向一致，非常重要！！！！！
            arc(t, r, a)
            t.lt(180-a)
        t.lt(360/p)
def move(t, length): # 一个画板画3朵花必须用暗中位移
    t.pu()
    t.fd(length)
    t.pd()
bob = turtle.Turtle()
move(bob, -100)
flower(bob, 7, 60, 60) # 偷偷设定半径和角度，万恶的例子，叫人怎么猜！于是我也直接搬！
move(bob, 100)
flower(bob, 10, 40, 80)
move(bob, 100)
flower(bob, 20, 140, 20)
turtle.mainloop()
标签：, , , , , , , , , , , , ,
还没有评论
2020-04
3

四行四列的小网格

By xrspook @ 22:17:26 归类于: 扮IT

先放效果图

Think Python 2 第三章练习题三我的解决办法。只能用学过的语句（还没讲到循环），for啊，while啊都不许用，于是我只能很蛮很直接了。如果要绘制两行两列的小网格，我只需把do_twice里的a、b函数从现在的重复4次变成重复两次即可。我觉得自己的脚本比官方提供的四行四列的小网格绘制法更易懂肿么破。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

def plus():
    print('+ ', end='')
def minus():
    print('- ' * 4, end='')
def bar():
    print('| ', end='')
def space():
    print('  ' * 4, end='')
def do_twice(a,b):
    a()
    b()
    a()
    b()
    a()
    b()
    a()
    b()
def do_four():
    col()
    col()
    col()
    col()
def col():
    do_twice(bar,space)
    bar()
    print('')    
def row():
    do_twice(plus,minus)
    plus()
    print('') 
def print_grid():
    do_twice(row,do_four)
    row()
print_grid()
标签：, , , , ,
2 条评论
1 … 3 4 5 6 7 8 9
© 2004 - 2024 我的天 | Theme by xrspook | Power by WordPress
Go to top